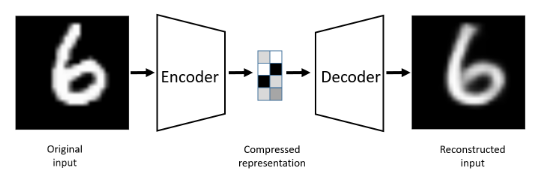
Autoencoders: Fundamentals of Encoders and Decoders Using Neural Nets
In the previous tutorials, we have talked about various neural nets architectures. In this tutorial, we will learn about Autoencoders and their application in machine learning. As we already know, dimensionality reduction is a crucial technique in machine learning and data science, used to simplify complex datasets while preserving their essential characteristics.
Two prominent methods for this task are Principal Component Analysis (PCA) and Autoencoders. While PCA is a traditional linear method, Autoencoders represent a more flexible, non-linear approach leveraging deep learning.
Principal Component Analysis is a linear dimensionality reduction technique that transforms a dataset into a new coordinate system. The new axes, called principal components, are ordered by the amount of variance they capture from the data. The goal of PCA is to reduce the dimensionality of the data while retaining as much variance as possible.
While PCA is powerful, it has several limitations:
- Interpretability: The principal components are linear combinations of the original features, which can sometimes be difficult to interpret.
- Linearity: PCA assumes that the data is linearly separable, which limits its effectiveness in capturing complex patterns in non-linear data.
- Global Variance: PCA captures global variance, which may not always align with the features most relevant to the specific task.
- PCA does scale well as the data size increases and may become computationally expensive.
Autoencoders offer a non-linear alternative to PCA, leveraging the power of neural networks to learn complex data representations. Unlike PCA, which is inherently linear, Autoencoders can capture non-linear relationships, making them more versatile for a broader range of applications.
Table of Contents
Prerequisites:
- Python, NumPy, Sklearn, Pandas and Matplotlib.
- Familiarity with TensorFlow and Keras
- Linear Algebra For Machine Learning.
- Statistics And Probability Theory.
- All of our previous machine-learning tutorials.
How Autoencoders Work:
Autoencoders consist of two main components:
1. Encoder: The encoder transforms the input data into a compressed, lower-dimensional representation. This is done by progressively reducing the number of neurons in each layer, leading to a “bottleneck” layer, which contains the most compressed version of the input.
- Input Layer: Takes the original data as input.
- Hidden Layers: Multiple layers of neurons that reduce the dimensionality.
- Bottleneck Layer: The final layer in the encoder, containing the compressed representation.
Let x be the input data, and z be the compressed representation. The encoder function can be represented as: z = f(x). Here, f represents the series of transformations (such as linear transformations followed by non-linear activations) that map the input x to the latent space z.
2. Decoder: The decoder reconstructs the original data from the compressed representation. It mirrors the encoder structure, gradually increasing the number of neurons in each layer until reaching the original input dimensions.
- Hidden Layers: Multiple layers that expand the dimensionality.
- Output Layer: The final layer that reconstructs the data in the original input space.
Let x’ be the reconstructed output. The decoder function can be represented as: x’ = g(z). Here, g represents the series of transformations that map the latent space z back to the reconstructed data x’.
Objective: Minimizing Reconstruction Error: The main objective in training an autoencoder is to minimize the difference between the input data and the reconstructed output. This difference is often measured using a loss function, such as the mean squared error (MSE) or binary cross-entropy.
The loss function can be written as: L = (1/n) * Σ (xi – x’i)^2
Here:
- L is the loss (reconstruction error).
- n is the number of data points.
- xi is the ith input data point.
- x’i is the ith reconstructed data point.
The goal is to adjust the parameters of the encoder (f) and decoder (g) such that the loss L is minimized. This ensures that the autoencoder learns to produce outputs x’ that are as close as possible to the original inputs x.
purpose of learning an “informative” representation of the data that
can be used for different applications by learning to reconstruct a set
of input observations well enough1
By compressing the data into a latent space, the autoencoder distills the most important features and patterns, which can then be leveraged for various downstream tasks. In an autoencoder, the goal is to learn a compressed representation of the input data. However, the model might simply learn to copy the input to the output, without extracting any meaningful information.
This may happen because the model’s objective is to minimize reconstruction error. Copying the input to the output achieves perfect reconstruction, hence a minimum error. The model becomes too closely fitted to the training data, capturing noise and irrelevant patterns instead of underlying structure.
To prevent the autoencoder from this, additional regularization techniques are employed during training. Regularization encourages the model to learn more meaningful and compact representations by imposing certain constraints. Some common regularization techniques include:
- Bottleneck Constraint: Limiting the size of the bottleneck layer (the latent representation) forces the model to compress the input data into a lower-dimensional space. This limitation makes it impossible for the model to simply copy the input data and encourages it to learn the most important features.
- Noise Injection (Denoising Autoencoders): By adding noise to the input data and training the autoencoder to reconstruct the original noise-free data, the model is discouraged from merely copying the input. Instead, it learns to focus on the underlying structure of the data, making it robust to noise.
- Sparse Regularization (Sparse Autoencoders): Adding a sparsity constraint, such as L1 regularization, encourages the activation of only a few neurons in the latent code. This forces the model to learn a more compact representation of the data, focusing on the most salient features.
Training of an Autoencoder
Autoencoders are trained using backpropagation(unsuprvised learning). The steps involved are:
- Input Data: The input data is fed into the encoder.
- Encoding: The encoder processes the input and generates a compressed representation (latent code / latent vector).
- Decoding: The decoder takes the latent code and tries to reconstruct the original input data.
- Reconstruction Error: The difference between the reconstructed output and the original input is calculated using a loss function (e.g., mean squared error).
- Backpropagation: The error is propagated backward through the network, updating the weights of both the encoder and decoder to minimize the reconstruction error.
Practical Applications of Autoencoders
Autoencoders have a wide range of applications, including:
- Data Compression: Reducing the dimensionality of data while preserving essential information, useful for storage and transmission. Also, by using the latent features, we can increase the time it takes to deal with high dimensional datasets in tasks like classification, however at reduced accuracy. Please note, it can only be used for the kind of data it was trained on.
- Anomaly Detection: By learning to reconstruct normal data, Autoencoders can identify anomalies that exhibit high reconstruction errors. However, you should keep in mind that the normal training data should not contain such outliers. Also, sometimes the results may be unstable, always verify or average the error using other models.
- Denoising: Removing noise from corrupted data, such as in images or audio signals.
- Feature Extraction: Learning useful features for tasks like classification or clustering.
Implementation Of Autoencoders
The architecture is very simple to understand and implement in practice. You can use any of the previous neural nets such as FNNs, CNNs or RNNs.
The goal is to create autoencoder = Model(inputs, decoder(encoder(inputs)), name = "autoencoder") and train the model. We first use encoder and choose a shape of the latent vector. Then we use this latent vector as input to the decoder to reconstruct the input. A detailed implementation of the autoencoders based on CNN is shown here on my GitHub, please refer to the code for better understanding. You can use ANNs as well.
In the first part of the code, the encoder compresses the input image into a lower-dimensional latent representation. This part consists of Conv2D layers which downsample the input image:
inputs = Input(shape=input_shape, name='encoder_input')
x = inputs
x = Conv2D(filters=32, kernel_size=3, activation="relu", strides=2, padding='same')(x)
x = Conv2D(filters=64, kernel_size=3, activation="relu", strides=2, padding="same")(x)
shape = K.int_shape(x)
x = Flatten()(x)
latent = Dense(latent_dim, name="latent_vector")(x)
Code language: Python (python)The decoder’s job is to take this latent representation and reconstruct the original image. This is where Conv2DTranspose layers come into play. They upsample the lower-dimensional latent representation back to the original image dimensions.
- Latent Input: The decoder takes the latent vector as input.
- Dense Layer: The latent vector is first passed through a Dense layer to expand it back to the shape before the Flatten layer in the encoder. This matches the shape that the Conv2DTranspose layers will expect.
- Reshape Layer: The output of the Dense layer is reshaped to match the shape of the last Conv2D layer’s output in the encoder.
- Conv2DTranspose Layers: These layers upsample the feature maps to gradually reconstruct the original input size.
- Output Layer: The final Conv2DTranspose layer produces the output image with a single channel and the same size as the input.
latent_inputs = Input(shape=(latent_dim,), name='decoder_input')
x = Dense(shape[1] * shape[2] * shape[3])(latent_inputs)
x = Reshape((shape[1], shape[2], shape[3]))(x)
x = Conv2DTranspose(filters=64, kernel_size=3, activation="relu", strides=2, padding="same")(x)
x = Conv2DTranspose(filters=32, kernel_size=3, activation="relu", strides=2, padding="same")(x)
outputs = Conv2DTranspose(filters=1, kernel_size=3, activation="sigmoid", padding="same", name="decoder_output")(x)
decoder = Model(latent_inputs, outputs, name="decoder")
Code language: JavaScript (javascript)And then we can create the autoencoder:
autoencoder = Model(inputs, decoder(encoder(inputs)), name = "autoencoder")
autoencoder.compile(loss = "mse", optimizer = "adam")
autoencoder.fit(x_train, x_train, validation_data = (x_test, x_test), epochs = 1, batch_size = batch_size)
autoencoder.predict(x_test)
Code language: JavaScript (javascript)This is how simple it is to create autoencoders.
Notes On Tranposed Convolutions
Also called fractionally strided convolutions are used to map data from a lower-dimensional space to a higher-dimensional space, while maintaining a connectivity pattern similar to that of normal convolutions.
In a standard convolution, the input data is convolved with a kernel to produce an output. This can be represented as a matrix multiplication where the input and output are unrolled into vectors.
- Input Matrix (I): Flattened to a vector.
- Kernel (W): Defines a sparse matrix (C) where non-zero entries correspond to the kernel elements.
- Output Vector (O): Result of the convolution.
The convolution operation can be represented as: O = C⋅I. Here, C is the matrix corresponding to the convolution operation, and I is the input vector. For backpropagation, the error is propagated by transposing the matrix C used in the forward pass: Error Gradient=CT ⋅ Loss. This ensures that the gradient is backpropagated through the network correctly.
A transposed convolution is essentially the reverse of a standard convolution. It maps a lower-dimensional space to a higher-dimensional space while maintaining the connectivity pattern.
- Forward Pass: Involves mapping from a compressed representation to an expanded one.
- Backward Pass: Involves mapping the gradient from the expanded space back to the compressed space.
Mathematical Representation: If a standard convolution is represented by multiplying with matrix C, the transposed convolution is represented by multiplying with CT, where CT is the transpose of matrix C. In practice, the operation can be described as:
- Forward Pass: Expanded Output = CT⋅Compressed Input
- Backward Pass: Gradient = C ⋅ Error Gradient
Consider a 2D convolution with a kernel and input of shape (3×3), producing an output of shape (2×2). If we want to use a transposed convolution to go from (2×2) back to (3×3), we use CT for the forward pass.
Implementing this operation directly as a convolution involves some additional steps: To emulate a transposed convolution using a standard convolution, you need to add rows and columns of zeros to the input. This increases the size of the input tensor to match the output dimensions desired from the transposed convolution.
After padding, you apply a standard convolution using a kernel that matches the desired output dimensions. This convolution operation effectively simulates the effect of a transposed convolution. Adding zeros increases the size of the input, which can lead to more computational overhead and memory usage.
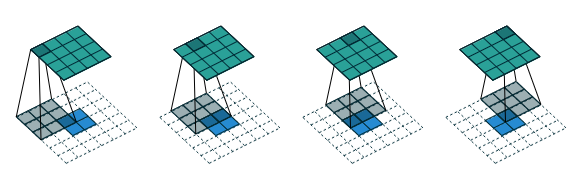
unit strides. It is equivalent to convolving a 3 × 3 kernel over a 2 × 2 input padded with a 2 × 2 border of zeros using unit strides. The transposed convolution does not guarantee to recover the input itself, as it is not defined as the inverse of the convolution, but rather just returns a feature map that has the same width and height.2
Keras, and other deep learning frameworks, employ more efficient algorithms to implement transposed convolutions. Instead of directly applying zero-padding and then performing standard convolution, Keras optimizes the kernel operations to directly compute the output without redundant calculations.
Denoising Autoencoders
Denoising Autoencoders (DAEs) are a variant of standard autoencoders that are specifically designed to handle noisy input data. Instead of learning to reconstruct the original input from a perfect copy, DAEs learn to reconstruct the original input from a corrupted or noisy version of it.
How it Works
- Corrupted Input: The input data is intentionally corrupted with noise (e.g., Gaussian noise).
- Encoding: The corrupted input is fed into the encoder, which maps it to a lower-dimensional latent space representation.
- Decoding: The decoder takes the latent representation and attempts to reconstruct the original, clean input data, ignoring the noise.
- Steps to Train a Denoising Autoencoder: Add Noise: Add some form of noise (e.g., Gaussian noise) to the original data. For example, if you have an image dataset, you can add random pixel noise to create a noisy version of the images. Model Training: Train the autoencoder on pairs of noisy and clean data. The input to the encoder is the noisy data, and the target output for the decoder is the clean data. Loss Function: Use a loss function that measures the reconstruction error, such as Mean Squared Error (MSE) between the clean data and the reconstructed output
For example, for MNIST dataset, you can add noise something like this:
noise = np.random.normal(loc = mean, scale = sigma, size = x_train.shape)
x_train_noisy = x_train + noise
and make sure to clip the values between 0 to 1 after adding noise on the normalized dataset otherwise the value may not be in 0 to 1 range.
x_train_noisy = np.clip(x_train_noisy, 0., 1.)
The training happens something like this,
autoencoder.compile(loss = "mse", optimizer = 'adam')
autoencoder.fit(x_train_noisy, x_train, validation_data = (x_test_noisy, x_test), epochs = 10, batch_size = batch_size)
Code language: JavaScript (javascript)The end to end implementation can be found here. Additonally, the same concept can be used to create colorization autoencoders (tranfering colors to grayscale images) as implemented here.
All you need to know is the basic concept of how to implement the autoencoders and how to adjust it to specific task. If you are stuck anywhere feel free to ask your doubts in the forum.
More of this later!
Further Readings:
Amritesh Kumar
I believe you are not dumb or unintelligent; you just never had someone who could simplify the concepts you struggled to understand. My goal here is to simplify AI for all. Please help me improve this platform by contributing your knowledge on machine learning and data science, or help me improve current tutorials. I want to keep all the resources free except for support and certifications. Email me @amriteshkr18@gmail.com.


